First Step to Lattice-based Cryptanalysis in SageMath

by Kurt Pan @ ZKPunk

Refs:

A Gentle Tutorial for Lattice-Based Cryptanalysis
Linear algebra and lattice reduction in Sage
Cryptanalysis on Lattice-Based Cryptography
Using Lattices for Cryptanalysis
Solving Hidden Number Problem with One Bit Oracle and Advice
Sage for Lattice-based Cryptography
https://www.latticechallenge.org/
https://lattice-estimator.readthedocs.io/en/latest/
The GGH Cryptosystem
Building Lattice Reduction (LLL) Intuition
LLL algorithm
COMPLEXITY OF LATTICE PROBLEMS: A Cryptographic Perspective Ch2
Mathematics of Public Key Cryptography. Version 2.0 by Steven D Galbraith

B  = matrix([[-2,2],[-2,1]])
B

[-2  2]
[-2  1]

B.LLL()

[ 0 -1]
[-2  0]

B.BKZ()

[ 0 -1]
[-2  0]

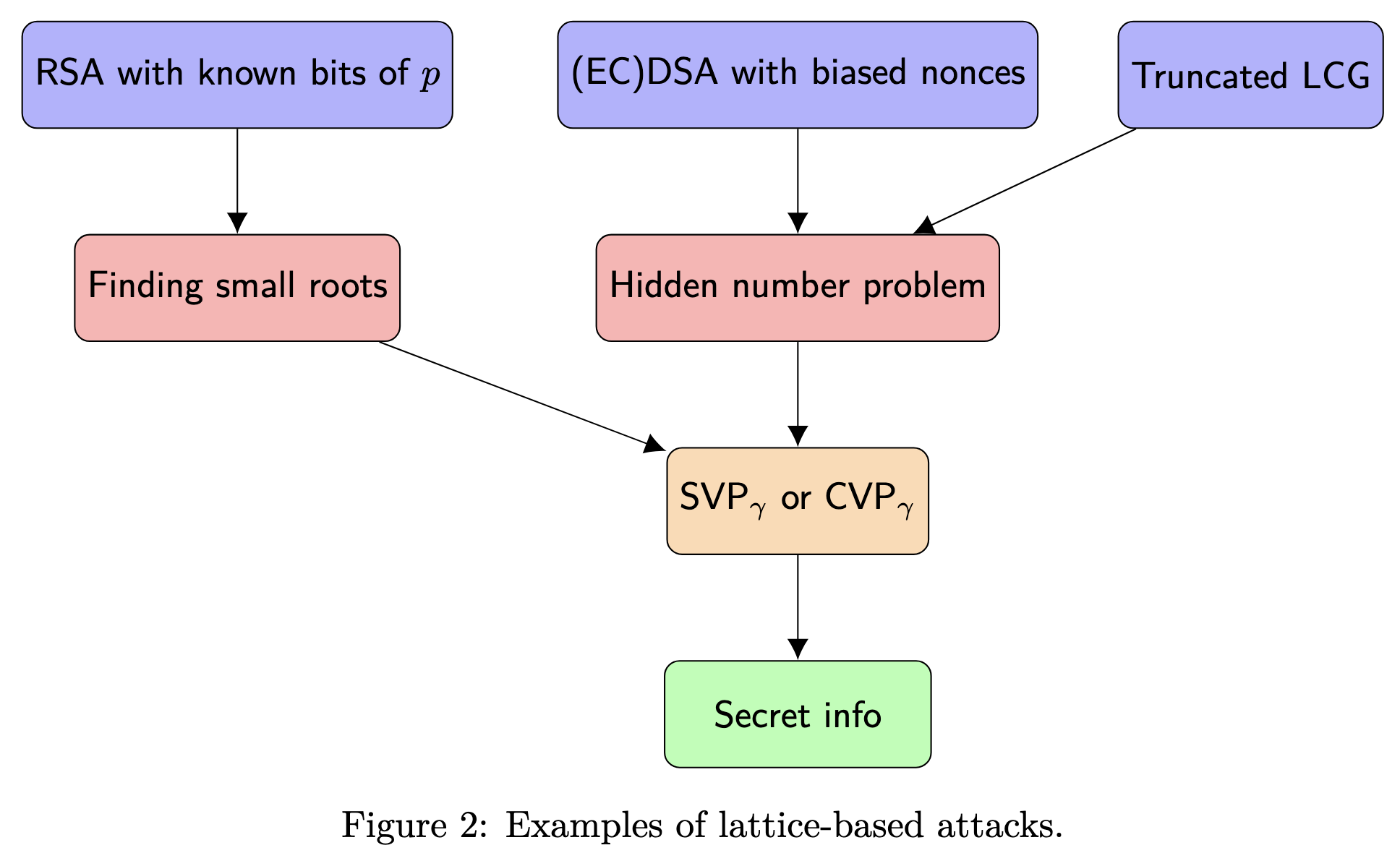
Lattice-based Attacks¶

Lattice-based attacks are attacks using lattices against cryptographic constructions.

ecdsa_nonce_hash_xor_privkey¶

ecdsa_nonce_hash_xor_privkey(Z, R, S, n)

Recovers the (EC)DSA private signing key given at least two messages and their signatures where the nonces $k_i$ were generated as $k_i = z_i \oplus d$ (i.e. message hash XOR private key).

Arguments:

• Z - A list of the message hashes $z_i$ .

• R - A list of the $r_i$ .

• S - A list of the $s_i$ .

• n - The modulus $n$ .

Returns:

The (EC)DSA private signing key $d$ .

from lbc_toolkit import ecdsa_nonce_hash_xor_privkey

# secp256k1
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f 
a, b = 0, 7 # y^2 = x^3 + 7
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
E = EllipticCurve(GF(p), [a, b])
G = E(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)

ell = 3
print(f'ECDSA k = z ⊕ d attack with ell = {ell}')
Z, R, S = [], [], []
d_ = randrange(1, n)
for i in range(ell):
    z = randrange(1, n)
    k = d_ ^^ z
    X = k * G
    r = int(X.xy()[0]) % n
    s = pow(k, -1, n) * (z + r * d_) % n
    Z.append(ZZ(z)); R.append(ZZ(r)); S.append(ZZ(s))
print(f'Z: {Z} \n R:{R} \n S:{S}')

ECDSA k = z ⊕ d attack with ell = 3
Z: [40158939334239771085186345813988284321475298553032946142808776308517126232355, 10263731867467130476891361419719020654219073006678761156220278659432100316638, 93832211787401370754669711158080455241827217904673492520835225409857942336754] 
 R:[3016406666953579940058863383656688008553852596293226998665092945776886933323, 69279327245905693223259736635726360553149755269876029627758104513351085078843, 68490791582828283666223591773824985479199669435248683540673615515308451261706] 
 S:[27085056783186418747293927485821318652836944183585344792065201605765516079507, 17061301929111395448998506435826410086768774467003804878022299949502444357524, 101211873492206722632384394957040415383702912523454995838975522107404845638258]

d = ecdsa_nonce_hash_xor_privkey(Z, R, S, n)
print('  Actual solution:', d_)
print('  Found  solution:', d)

[subset_sum] Density: 0.3333
[subset_sum] Lattice dimensions: (260, 260)
[subset_sum] Lattice reduction took 6.938s
  Actual solution: 94893380599505757455235797215681909011099659696076178403734478274118865679913
  Found  solution: 94893380599505757455235797215681909011099659696076178403734478274118865679913

def demo_ecdsa_nonce_hash_xor_privkey(Z, R, S, n):
    jth_bit = lambda x, j: (x >> j) & 1

    ell = len(Z)
    m = n.nbits()
    P = PolynomialRing(GF(n), [f'd{j}' for j in range(m)])
    d_bits = list(P.gens())
    d = sum(2^j * d_bits[j] for j in range(m))

    weights = []
    targets = []
    for i in range(ell):
        k_i = Z[i] + d - 2 * sum(2^j * jth_bit(Z[i], j) * d_bits[j] for j in range(m))
        eq = S[i] * k_i - (Z[i] + R[i] * d)
        coeffs = [c for c, _ in eq]
        weights.append([ZZ(x) for x in coeffs[:-1]])
        targets.append(-ZZ(coeffs[-1]))

    sol = subset_sum(weights, targets, n, verbose=True)
    d = int(''.join(map(str, sol))[::-1], 2)
    return d

ecdsa_biased_nonce¶

ecdsa_biased_nonce_zero_msb(Z, R, S, n, l)
ecdsa_biased_nonce_zero_lsb(Z, R, S, n, l)
ecdsa_biased_nonce_known_msb(Z, R, S, T, n, l)
ecdsa_biased_nonce_shared_msb(Z, R, S, n, l)

Implementation of a few different variations of attacks against (EC)DSA with biased nonces as described in [HS01]. The signatures satisfy the DSA equation

s_i = k_i^{-1}(z_i + r_i d) \pmod n

(1)

Given many messages $z_i$ and their signatures $(r_i, s_i)$ calculated with the biased nonces $k_i$ , the private signing key $d$ may be recovered.

Arguments:

• Z - A list of the message hashes $z_i$ .

• R - A list of the $r_i$ .

• S - A list of the $s_i$ .

• n - The modulus $n$ .

• l - The number of bits of bias.

In the ecdsa_biased_nonce_known_msb function, the argument T is the list of known MSBs of each $k_i$ .

Returns:

The (EC)DSA private signing key $d$ .

Lattice-based Problems¶

Knapsack Problem¶

The knapsack problem is a well-known NP-complete computational problem that has been used as a trapdoor in some public key cryptosystems [MH78, CR88, Yas07]. The most common version of the knapsack problem in cryptography and cryptanalysis is the subset sum problem which involves finding a subset of a given set of numbers that sum to a given target.

subset_sum(weights, targets, modulus=None, N=None, lattice_reduction=None, verbose=False)

Finds the solution of the subset sum problem with the given weights and targets. Supports multiple knapsacks as well as the modular case with the modulus argument.

Arguments:

• weights - A list of integer weights $a_1, \ldots, a_n$ , or a list of lists $a_{1, 1}, \ldots, a_{k, n}$ for the multiple subset sum problem with $k$ different subset sums.

• targets - The integer target $s$ , or a list of targets $s_1, \ldots, s_j$ for the multiple subset sum problem case.

• modulus - (optional) The modulus $M$ .

• N - (optional) The scaling factor $N$ as described in [PZ16]. (Default: $\lceil \sqrt{(n+1)/4} \rceil$ )

Returns:

A solution to the given subset sum problem as a list representing the $e_i$ such that

\sum_{i=1}^n e_i a_{j, i} = s_j

(2)

for all $1 \leq j \leq k$ .

The density of the multiple modular subset sum problem is defined as $d=\frac{n}{k \cdot \log _2 M}$ .

from sage.modules.free_module_integer import IntegerLattice
from lbc_toolkit import subset_sum

def multiple_modular_subset_sum_example():
    print('Multiple Modular Subset Sum Example')
    U, M, k, n = 2^80, 2^80, 6, 100
    weights = [[randint(0, U) for _ in range(n)] for _ in range(k)]
    e = [randint(0, 1) for _ in range(n)]
    targets = [sum([e * a for e, a in zip(e, W)]) % M for W in weights]
    sol = subset_sum(weights, targets, modulus=M, verbose=True)
    assert sol
    assert all(targets[j] == sum([e * a for e, a in zip(sol, weights[j])]) % M for j in range(k))
    print('  Actual solution:', e)
    print('  Found  solution:', sol, end='\n\n')

multiple_modular_subset_sum_example()

Multiple Modular Subset Sum Example
[subset_sum] Density: 0.2083
[subset_sum] Lattice dimensions: (107, 107)
[subset_sum] Lattice reduction took 0.987s
  Actual solution: [0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1]
  Found  solution: [0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1]

$N>\sqrt{\frac{n+1}{4}}$

Example: n=2, k=1

Modular equation: 3e₁ + 5e₂ ≡ 8 (mod 10), solution: e₁=1, e₂=1

Lattice basis B’ (with N=2):

[1 0 0 6 ] ← I_n and Na_{1,1}=2×3

[0 1 0 10 ] ← I_n and Na_{1,2}=2×5

[0 0 0 20 ] ← NM=2×10

[1/2 1/2 1/2 16 ] ← 1/2 and Ns₁=2×8

Linear combination: (1, 1, 0, -1)

1×row1 = (1, 0, 0, 6)
1×row2 = (0, 1, 0, 10)
0×row3 = (0, 0, 0, 0)
-1×row4 = (-1/2, -1/2, -1/2, -16)

Sum: (1/2, 1/2, -1/2, 6+10-16) = (1/2, 1/2, -1/2, 0)

Last coordinate is 0 because:

3×1 + 5×1 = 8 = 8 + 0×10
So ℓ₁ = 0
N(3+5) - 0×N×10 - N×8 = N×8 - N×8 = 0 ✓

def demo_subset_sum(weights, targets, modulus=None, N=None, lattice_reduction=None, verbose=False):
    verbose = (lambda *a: print('[subset_sum]', *a)) if verbose else lambda *_: None

    if type(weights[0]) is list:
        k = len(weights)
        n = len(weights[0])
    else:
        k = 1
        n = len(weights)
        weights = [weights]
        targets = [targets]

    if modulus is not None:
        density = n / (k * log(modulus, 2))
    else:
        density = n / (k * log(max(flatten(weights)), 2))
    verbose('Density:', round(density.n(), 4))

    N = N or ceil(sqrt((n+1)/4))
    B = 2 * Matrix.identity(n)
    B = B.augment(vector([0] * n))
    for j in range(k):
        B = B.augment(vector([N * a for a in weights[j]]))
    if modulus is not None:
        B = B.stack(Matrix.zero(k, n + 1).augment(N * modulus * Matrix.identity(k)))
    B = B.stack(vector([1] * (n + 1) + [N * s for s in targets]))

    verbose('Lattice dimensions:', B.dimensions())
    lattice_reduction_timer = cputime()
    if lattice_reduction:
        B = lattice_reduction(B)
    else:
        B = B.LLL()
    verbose(f'Lattice reduction took {cputime(lattice_reduction_timer):.3f}s')

    for row in B:
        if row[n] < 0:
            sol = [(x + 1)//2 for x in row[:n]]
        else:
            sol = [(1 - x)//2 for x in row[:n]]
        if any(x not in [0, 1] for x in sol):
            continue
        for j in range(k):
            t = sum(e * a for e, a in zip(sol, weights[j]))
            tj = targets[j]
            if modulus > 0:
                t %= modulus
                tj %= modulus
            if t != tj:
                break
        else:
            return sol
        
    return None

Hidden Number Problem¶

Let $p$ be a prime and let $\alpha \in[1, p-1]$ be a secret integer. Recover $\alpha$ given $m$ pairs of integers $\left\{\left(t_i, a_i\right)\right\}_{i=1}^m$ such that

\beta_i-t_i \alpha+a_i=0 \quad(\bmod p)

(3)

where the $\beta_i$ are unknown and satisfy $\left|\beta_i\right|<B$ for some $B<p$ .

from lbc_toolkit import hnp, ehnp
print('HNP Example')
p, m, B = random_prime(2^10), 2, 2^3
#_alpha = randrange(1, p)
_alpha = 666
T = [randrange(1, p) for _ in range(m)]
_Beta = [randrange(0, B) for _ in range(m)]
A = [(t * _alpha - beta) % p for t, beta in zip(T, _Beta)]
sol = hnp(p, T, A, B, verbose=True)
print('  Actual solution:', _alpha)
print('  Found  solution:', sol, end='\n\n')

HNP Example
[hnp] Lattice dimensions: (4, 4)
[hnp] Lattice reduction took 0.003s
  Actual solution: 666
  Found  solution: 666

def demo_hnp(p, T, A, B, lattice_reduction=None, verbose=False):
    r"""
    Returns the solution of the given hidden number problem instance. i.e. finds
    `\alpha \in [1, p - 1]` satisfying

    .. MATH::

        \beta_i - t_i \alpha + a_i \equiv 0 \pmod p

    where the `t_i` and `a_i` are given by ``T`` and ``A``, and the `\beta_i`
    are bounded above by ``B``.
    """

    verbose = (lambda *a: print('[hnp]', *a)) if verbose else lambda *_: None

    if len(T) != len(A):
        raise ValueError(f'Expected number of t_i to equal number of a_i, but got {len(T)} and {len(A)}.')

    m = len(T)
    M = p * Matrix.identity(QQ, m)
    M = M.stack(vector(T))
    M = M.stack(vector(A))
    M = M.augment(vector([0] * m + [B / p] + [0]))
    M = M.augment(vector([0] * (m + 1) + [B]))
    M = M.dense_matrix()

    verbose('Lattice dimensions:', M.dimensions())
    lattice_reduction_timer = cputime()
    if lattice_reduction:
        M = lattice_reduction(M)
    else:
        M = M.LLL()
    verbose(f'Lattice reduction took {cputime(lattice_reduction_timer):.3f}s')

    for row in M:
        if row[-1] == -B:
            alpha = (row[-2] * p / B) % p
            if all((beta - t * alpha + a) % p == 0 for beta, t, a in zip(row[:m], T, A)):
                return alpha
        if row[-1] == B:
            alpha = (-row[-2] * p / B) % p
            if all((beta - t * alpha + a) % p == 0 for beta, t, a in zip(-row[:m], T, A)):
                return alpha

    return None

Lattice ALgorithms¶

The LLL Algorithm¶

Let $\mathbf{B}=\left\{\mathbf{b}_1, \mathbf{b}_2\right\}$ where $\mathbf{b}_1=(-2,2), \mathbf{b}_2=(-2,1)$ . We will run the LLL algorithm on this lattice basis, using $\delta=0.75$

both algorithms use a reduce-and-then-swap technique to achieve their goals.
We can roughly say that LLL is an extension of Euclid’s algorithm that applies to a set of $n$ -vectors instead of integers.
LLL extends Gauss’ algorithm for reduction to work with $n$ vectors.
Round version of GSO

def project(v, u):
    """Project vector v onto vector u"""
    if u.dot_product(u) == 0:
        return vector([0] * len(v))  # Handle zero vector case
    return (v.dot_product(u) / u.dot_product(u)) * u

# Usage
v = vector([2, 2])
u = vector([3, 1])
proj = project(v, u)
proj

(12/5, 4/5)

B  = matrix([[-2,2],[-2,1]])
G, M = B.gram_schmidt()
B,G

(
[-2  2]  [  -2    2]
[-2  1], [-1/2 -1/2]
)

B.LLL()

[ 0 -1]
[-2  0]

def plot_2d_lattice(v1, v2, xmin=-10, xmax=10, ymin=-10, ymax=10, show_basis_vectors=True):
    """
    sage plot of a lattice with v1 and v2 as basis vectors.
    """

    pts = []
    # plot all integer multiples of the basis so long as the x and y coordinates
    # are within (x|y)(min|max).
    for i in range(xmin, xmax):
        for j in range(ymin, ymax):
            pt = i*v1 + j*v2
            x,y = pt[0], pt[1]
            if x < xmin or x > xmax or y < ymin or y > ymax:
                continue
            pts.append(pt)
    the_plot = plot(points(pts))
    if show_basis_vectors:
        the_plot += plot(v1) + plot(v2)
    return the_plot

v1 = vector(ZZ, [3,5])
v2 = vector(ZZ, [8,3])
V  = Matrix(ZZ, [v1,v2])
Vr,_ = V.gram_schmidt()
pplot = plot_2d_lattice(V[0], V[1])
pplot += plot(Vr[0], color='grey', linestyle='-.', legend_label='unmodified', legend_color='blue')
pplot += plot(Vr[1], color='grey', linestyle='-.', legend_label='orthogonalized', legend_color='grey')
pplot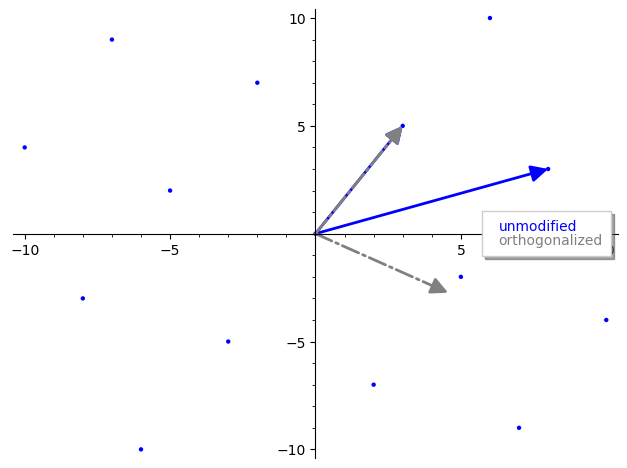

Graphics object consisting of 5 graphics primitives

Vr

[     3      5]
[155/34 -93/34]

Solving CVP¶

Babai’s Nearest Plane Algorithm¶

from sage.modules.free_module_integer import IntegerLattice
B = Matrix(ZZ, [[0, 2], [2, 1]])
L = IntegerLattice(B)
target = vector(QQ, [3.5, 3.5])
closest = L.closest_vector(target)
closest

(4, 4)

Cryptography

FHE

Cryptanalysis

fpylll: A Python Interface to the fplll Lattice Reduction Library